开篇
一位程序员曾问我一个很简单的问题:“怎样给一个磁盘文件排序?”想当年我是一上来就犯了错误,现在,在讲这个故事之前,先给大家一个机会,看看能否比我当年做得更好。你会怎样回答上述问题呢?
一次友好的对话
我错就错在马上回答了这个问题。我告诉他一些有关如何在磁盘 上实现归并排序的简要思路。我建议他深入研究算法教材,他似乎不 太感冒。他更关心如何解决这个问题,而不是深入学习。于是我告诉 他在一本流行的程序设计书里有磁盘排序的程序。那个程序有大约200 行代码和十几个函数,我估计他最多需要一周时间来实现和测试该代 码。
我以为已经解决了他的问题,但是他的踌躇使我返回到了正确的 轨道上。其后就有了下面的对话,楷体部分是我的问题。
为什么非要自己编写排序程序呢?为什么不用系统提供的排序功 能呢?
我需要在一个大系统中排序。由于不明的技术原因,我不能使用 系统中的文件排序程序。
需要排序的内容是什么?文件中有多少条记录?每条记录的格式 是什么?
文件最多包含1千万条记录,每条记录都是7位的整数。
等一下,既然文件这么小,何必非要在磁盘上进行排序呢?为什 么不在内存里进行排序呢?
尽管机器有许多兆字节的内存,但排序功能只是大系统中的一部 分,所以,估计到时只有1 MB的内存可用。
你还能告诉我其他一些与记录相关的信息吗?
每条记录都是7位的正整数,再无其他相关数据。每个整数最多只 出现一次。
这番对话让问题更明确了。在美国,电话号码由3位“区号”后再跟 7位数字组成。拨打含“免费”区号800(当时只有这一个号码)的电话 是不收费的。实际的免费电话号码数据库包含大量的信息:免费电话 号码、呼叫实际中转到的号码(有时是几个号码,这时需要一些规则 来决定哪些呼叫在什么时间中转到哪里)、主叫用户的姓名和地址 等。
这位程序员正在开发这类数据库的处理系统的一小部分,需要排 序的整数就是免费电话号码。输入文件是电话号码的列表(已删除所 有其他信息),号码重复出现算出错。期望的输出文件是以升序排列 的电话号码列表。应用背景同时定义了相应的性能需求。当与系统的 会话时间较长时,用户大约每小时请求一次有序文件,并且在排序未 完成之前什么都干不了。因此,排序最多只允许执行几分钟,10秒钟 是比较理想的运行时间。
准确的问题描述
对程序员来说,这些需求加起来就是:“如何给磁盘文件排序?” 在试图解决这个问题之前,先将已知条件组织成一种更客观、更易用 的形式。
输入:一个最多包含 n 个正整数的文件,每个数都小于 n,其中
n=107 。如果在输入文件中有任何整数重复出现就是致命错误。没有其
他数据与该整数相关联。
输出:按升序排列的输入整数的列表。
约束:最多有(大约)1 MB的内存空间可用,有充足的磁盘存储
空间可用。运行时间最多几分钟,运行时间为10秒就不需要进一步优
化了。请花上一分钟思考一下该问题的规范说明。现在你打算给程序员 什么样的建议呢?
程序设计
显而易见的方法是以一般的基于磁盘的归并排序程序为起点,但 是要对其进行调整,因为我们是对整数进行排序。这样就可以将原来 的200行程序减少为几十行,同时也使得程序运行得更快,但是完成程 序并使之运行可能仍然需要几天的时间。
另一种解决方案更多地利用了该排序问题的特殊性。如果每个号 码都使用7个字节来存储,那么在可用的1 MB存储空间里大约可以存 143 000个号码。如果每个号码都使用32位整数来表示的话,在1 MB存 储空间里就可以存储250 000个号码。因此,可以使用遍历输入文件40 趟的程序来完成排序。在第一趟遍历中,将0至249 999之间的任何整数 都读入内存,并对这(最多)250 000 个整数进行排序,然后写到输出 文件中。第二趟遍历排序250 000至499 999之间的整数,依此类推,到 第40趟遍历的时候对9 750 000至9 999 999之间的整数进行排序。对内 存中的排序来说,快速排序会相当高效,而且仅仅需要20 行代码(见 第11章)。于是,整个程序就可以通过一两页纸的代码实现。该程序 拥有所期望的特性——不必考虑使用中间磁盘文件;但是,为此所付 出的代价是要读取输入文件40次。
归并排序读入输入文件一次,然后在工作文件的帮助下完成排序 并写入输出文件一次。工作文件需要多次读写。
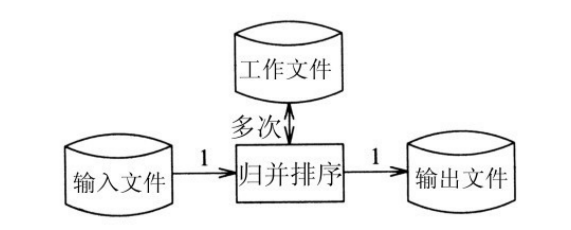
40趟算法读入输入文件多次,写输出文件仅一次,不使用中间文 件。

下图所示的方案更可取。我们结合上述两种方法的优点,读输入 文件仅一次,且不使用中间文件。
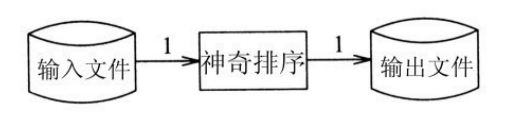
只有在输入文件中的所有整数都可以在可用的1 MB内存中表示的 时候才能够实现该方案。于是问题就归结为是否能够用大约800万个可 用位来表示最多1 000万个互异的整数。考虑一种合适的表示方式。
实现概要
由是观之,应该用位图或位向量表示集合。可用一个 20 位长的字 符串来表示一个所有元素都小于 20 的简单的非负整数集合。例如,可 以用如下字符串来表示集合{1,2,3,5,8,13}:0 1 1 1 0 1 0 0 1 0 0 0 0 1 0 0 0 0 0 0
代表集合中数值的位都置为1,其他所有的位都置为0。
在我们的实际问题中,每个7位十进制整数表示一个小于1 000万的 整数。我们使用一个具有1 000万个位的字符串来表示这个文件,其 中,当且仅当整数i在文件中存在时,第i位为1。(那个程序员后来找 到了200万个稀疏位,习题5研究了最大存储空间严格限制为1 MB的情 况。)这种表示利用了该问题的三个在排序问题中不常见的属性:输 入数据限制在相对较小的范围内;数据没有重复;而且对于每条记录 而言,除了单一整数外,没有任何其他关联数据。
若给定表示文件中整数集合的位图数据结构,则可以分三个自然 阶段来编写程序。第一阶段将所有的位都置为 0,从而将集合初始化为 空。第二阶段通过读入文件中的每个整数来建立集合,将每个对应的 位都置为1。第三阶段检验每一位,如果该位为1,就输出对应的整 数,由此产生有序的输出文件。令n为位向量中的位数(在本例中为10 000 000),程序可以使用伪代码表示如下:
/* phase 1: initialize set to empty */
for i = [0,n)
bit[i] = 0
/* phase 2: insert present elements into the set */
for each i in the input file
bit[i] = 1
/* phase 3: write sorted output */
for i = [0,n)
if bit[i] == 1
write i on the output file
(回想在前言中所提到的,for i=[0,n)表示在从0至n-1的范围内对i
进行迭代。)这个实现概要已经足以解决那个程序员的问题了。习题2、习题5 和习题7描述了他会遇到的一些实现细节。
原理
那个程序员打电话把他的问题告诉我,然后我们花了大约一刻钟 时间明确了问题所在,并找到了位图解决方案。他花了几个小时来实 现这个几十行代码的程序。该程序远远优于我们在电话刚开始时所担 心的需要花费一周时间编写的几百行代码的那个程序。而且程序执行 得很快:磁盘上的归并排序可能需要许多分钟的时间,该程序所需的 时间只比读取输入和写入输出所需的时间多一点点——大约 10 秒钟。 答案 3包含了对完成该任务的几种不同程序的计时细节。
从这些事实中可以总结出该实例研究所得到的第一个结论:对小 问题的仔细分析有时可以得到明显的实际益处。在该实例中,几分钟 的仔细研究可以大幅削减代码的长度、程序员时间和程序运行时间。 Chuck Yeager将军(第一个超音速飞行的人)赞扬一架飞机的机械系统 时用的词是“结构简单、部件很少、易于维护、非常坚固”,该程序拥 有同样的属性。然而,当规范说明的某些因素发生改变时,该程序的 特殊结构将很难修改。除了需要精巧的编程以外,该实例阐明了如下 一般原理。
正确的问题。明确问题,这场战役就成功了90%——我很庆幸程序 员没有满足于我给出的第一个程序。一旦正确理解了问题,习题10、 习题11和习题12的答案都会很优雅。在查看提示和答案以前,请努力 思考这些问题。
位图数据结构。该数据结构描述了一个有限定义域内的稠密集 合,其中的每一个元素最多出现一次并且没有其他任何数据与该元素 相关联。即使这些条件没有完全满足(例如,存在重复元素或额外的 数据),也可以用有限定义域内的键作为一个表项更复杂的表格的索 引,见习题6和习题8。
多趟算法。这些算法多趟读入其输入数据,每次完成一步。在1.3 节已经见到了一个40趟算法,习题5鼓励读者去完成一个两趟算法。 时间—空间折中与双赢。编程文献和理论中充斥着时间—空间的 折中:通过使用更多的时间,可以减少程序所需的空间。例如,答案5 中的两趟算法让程序运行时间加倍从而使空间减半。但我的经验常常 是这样的:减少程序的空间需求也会减少其运行时间。 [1] 空间上高效 的位图结构显著地减少了排序的运行时间。空间需求的减少之所以会 导致运行时间的减少,有两个原因:需要处理的数据变少了,意味着 处理这些数据所需的时间也变少了;同时将这些数据保存在内存中而 不是磁盘上,进一步避免了磁盘访问的时间。当然了,只有在原始的 设计远非最佳方案时,才有可能时空双赢。
简单的设计。Antoine de Saint-Exupéry是法国作家兼飞机设计师, 他曾经说过:“设计者确定其设计已经达到了完美的标准不是不能再增 加任何东西,而是不能再减少任何东西。”更多的程序员应该使用该标 准来检验自己完成的程序。简单的程序通常比具有相同功能的复杂的 程序更可靠、更安全、更健壮、更高效,而且易于实现和维护。 程序设计的阶段。这个实例揭示了12.4节详细描述的设计过程。
习题
部分习题的提示和答案可以在本书后面找到。
- 如果不缺内存,如何使用一个具有库的语言来实现一种排序算法 以表示和排序集合?
- 如何使用位逻辑运算(如与、或、移位)来实现位向量?
- 运行时效率是设计目标的一个重要组成部分,所得到的程序需要 足够高效。在你自己的系统上实现位图排序并度量其运行时间。该时 间与系统排序的运行时间以及习题1中排序的运行时间相比如何?假设 n为10 000 000,且输入文件包含1 000 000个整数。
- 如果认真考虑了习题3,你将会面对生成小于n且没有重复的k个 整数的问题。最简单的方法就是使用前k个正整数。这个极端的数据集 合将不会明显地改变位图方法的运行时间,但是可能会歪曲系统排序 的运行时间。如何生成位于0至n-1之间的k个不同的随机顺序的随机整 数?尽量使你的程序简短且高效。
- 那个程序员说他有1 MB的可用存储空间,但是我们概要描述的 代码需要1.25 MB的空间。他可以不费力气地索取到额外的空间。如果 1 MB空间是严格的边界,你会推荐如何处理呢?你的算法的运行时间 又是多少?
- 如果那个程序员说的不是每个整数最多出现一次,而是每个整数 最多出现10次,你又如何建议他呢?你的解决方案如何随着可用存储 空间总量的变化而变化?
- [R.Weil]本书1.4节中描述的程序存在一些缺陷。首先是假定在输 入中没有出现两次的整数。如果某个数出现超过一次的话,会发生什 么?在这种情况下,如何修改程序来调用错误处理函数?当输入整数 小于零或大于等于n时,又会发生什么?如果某个输入不是数值又如 何?在这些情况下,程序该如何处理?程序还应该包含哪些明智的检 查?描述一些用以测试程序的小型数据集合,并说明如何正确处理上 述以及其他的不良情况。
- 当那个程序员解决该问题的时候,美国所有免费电话的区号都是 800。现在免费电话的区号包括800、877和888,而且还在增多。如何 在1 MB空间内完成对所有这些免费电话号码的排序?如何将免费电话 号码存储在一个集合中,要求可以实现非常快速的查找以判定一个给 定的免费电话号码是否可用或者已经存在?
- 使用更多的空间来换取更少的运行时间存在一个问题:初始化空 间本身需要消耗大量的时间。说明如何设计一种技术,在第一次访问 向量的项时将其初始化为0。你的方案应该使用常量时间进行初始化和 向量访问,使用的额外空间应正比于向量的大小。因为该方法通过进 一步增加空间来减少初始化的时间,所以仅在空间很廉价、时间很宝 贵且向量很稀疏的情况下才考虑使用。
- 在成本低廉的隔日送达时代之前,商店允许顾客通过电话订购 商品,并在几天后上门自取。商店的数据库使用客户的电话号码作为 其检索的主关键字(客户知道他们自己的电话号码,而且这些关键字 几乎都是唯一的)。你如何组织商店的数据库,以允许高效的插入和 检索操作?
- 在20世纪80年代早期,洛克希德公司加利福尼亚州桑尼维尔市 工厂的工程师们每天都要将许多由计算机辅助设计(CAD)系统生成 的图纸从工厂送到位于圣克鲁斯市的测试站。虽然仅有40公里远,但 使用汽车快递服务每天都需要一个多小时的时间(由于交通阻塞和山 路崎岖),花费100美元。请给出新的数据传输方案并估计每一种方案 的费用。
- 载人航天的先驱们很快就意识到需要在外太空的极端环境下实 现顺利书写。民间盛传美国国家宇航局(NASA)花费100万美元研发 出了一种特殊的钢笔来解决这个问题。那么,前苏联又会如何解决相 同的问题呢?
深入阅读
这个小练习仅仅是令人痴迷的程序说明问题的冰山一角。要深入 研 究 这 个 重 要 的 课 题 , 参 见 Michael Jackson [2] 的 Software Requirements & Specifications 一书(Addison-Wesley 出版社 1995 年出 版)。该书用一组独立成章却又相辅相成的短文,以令人愉悦的方式 阐述了这个艰涩的课题。
在本章所描述的实例研究中,程序员的主要问题与其说是技术问 题,还不如说是心理问题:他不能解决问题,是因为他企图解决错误 的问题。问题的最终解决,是通过打破他的概念壁垒,进而去解决一 个 较 简 单 的 问 题 而 实 现 的 。 James L.Adams 所 著 的 Conceptuel Blockbusting一书(第3版由Perseus出版社于1986年出版)研究了这类跳 跃,该书通常是触发创新性思维的理想选择。虽然该书不是专为程序 员而写的,其中的许多内容却特别适用于编程问题。Adams将概念壁垒 定义为“阻碍解题者正确理解问题或取得答案的心智壁垒”。习题10、 习题11和习题12激励读者去打破一些这样的壁垒。